Social Data Science

Statistical Reasoning: Interpreting Patterns in Data

Olgahan Çat (olgahan@brown.edu)

Goals

Find out whether data automatically tells us what is true or not
Identify patterns in data and describe what they show
Distinguish descriptive, predictive, and causal claims
Ask better questions when someone makes a data-based claim

Why statistical reasoning matters?

Intellectual skill: Reason carefully about patterns in human behavior
Academia: Read, interpret, and contribute to social science research
Policy: Evaluate evidence behind decisions that affect society
Private sector & life: Use data responsibly to anticipate outcomes

“According to data…”

Does data speak?

Common claims:
- “The data says X causes Y”
- “According to data, A is better than B”
Implied: data reveals objective truth
Reality: data requires interpretation

Variables

Characteristics that vary

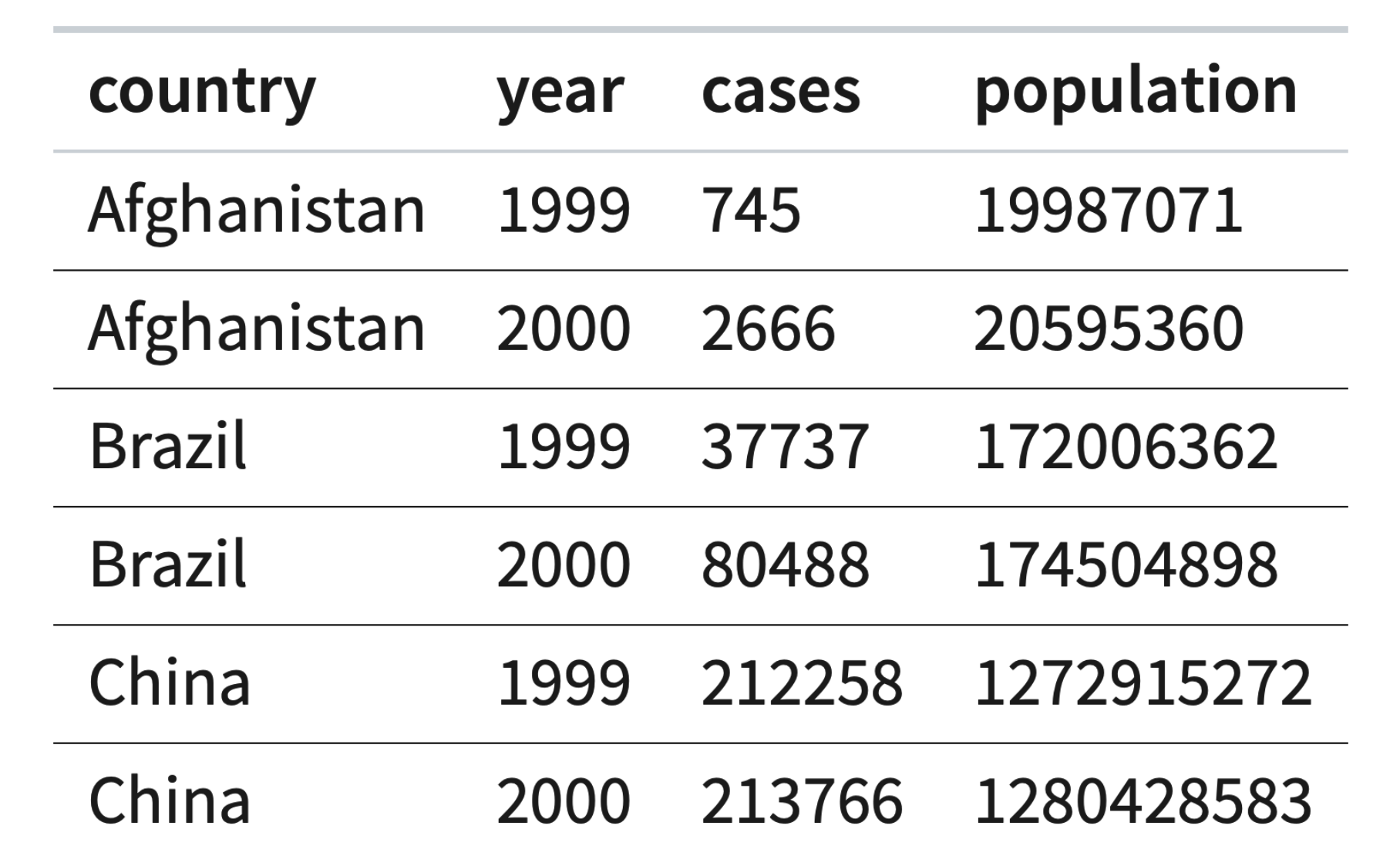
Types of Variables

Nominal/categorical: Cannot be ordered
- Region
Ordinal: Ordered
- Very liberal < Liberal < Moderate < Conservative < Very conservative -Numerical: Ordered + equidistant
- Age, GDP, number of casualties

Practice

Varieties of Democracy’s regime type measure:

0: Closed autocracy – No multiparty elections
1: Electoral autocracy – De-jure elections but not free and fair
2: Electoral democracy – Free and fair elections with some flaws
3: Liberal democracy – Free and fair elections guaranteed

Political Regimes

Interactive Map

Descriptive Statistics

Summarizing Patterns: Categorical data

Counts / frequencies: How many observations fall in each category.
Percentages / proportions: Useful to compare groups.
Mode: The most common category

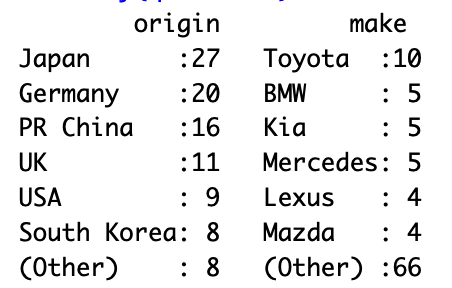Source: qatarcars

Descriptive Statistics

Summarizing Patterns: Numerical data

Measures of central tendency:
- Mean (average): Add values, divide by count
- Median: Middle value when ordered
- Mode: Most common value
Measures of spread / variability:
- Range: Difference between max and min
- Standard deviation

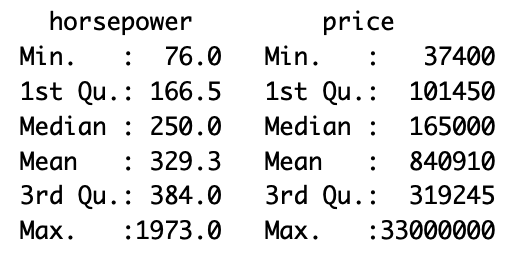Source: qatarcars

Predictive Reasoning

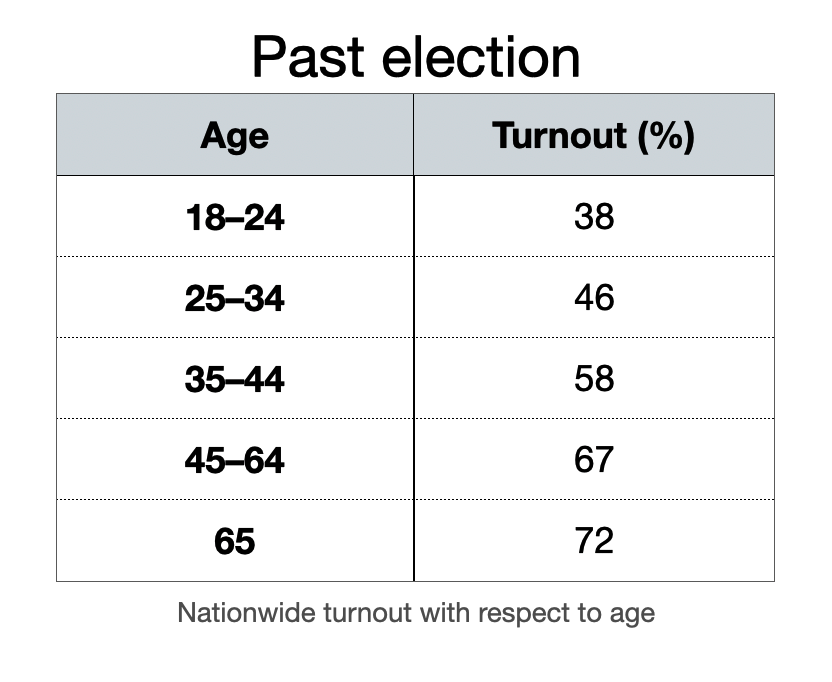
Can we forecast outcomes?

Use patterns to predict an outcome
Example: Next election, would we expect a high or low turnout at a university town?
What if we want to know why?

Causal Inference

Does X cause Y?

X: Independent variable
Y: Dependent variable
Causal claims are everywhere
The ultimate question:
- does changing X change Y

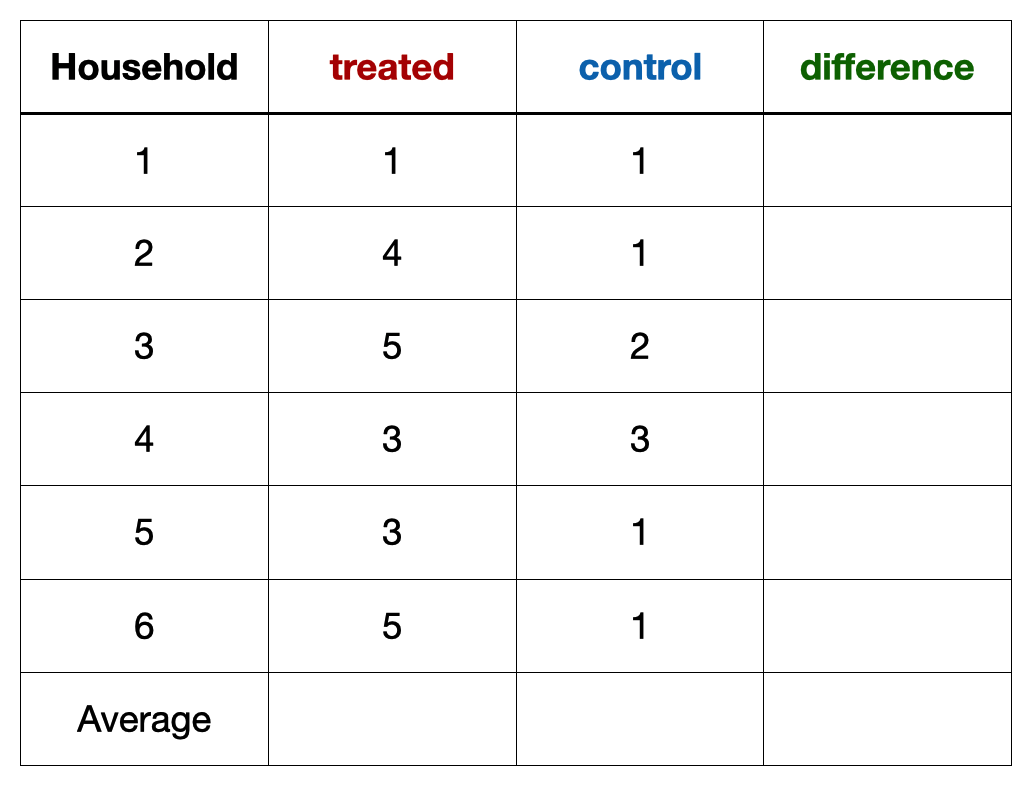
Do democracy promotion programs reduce protests?

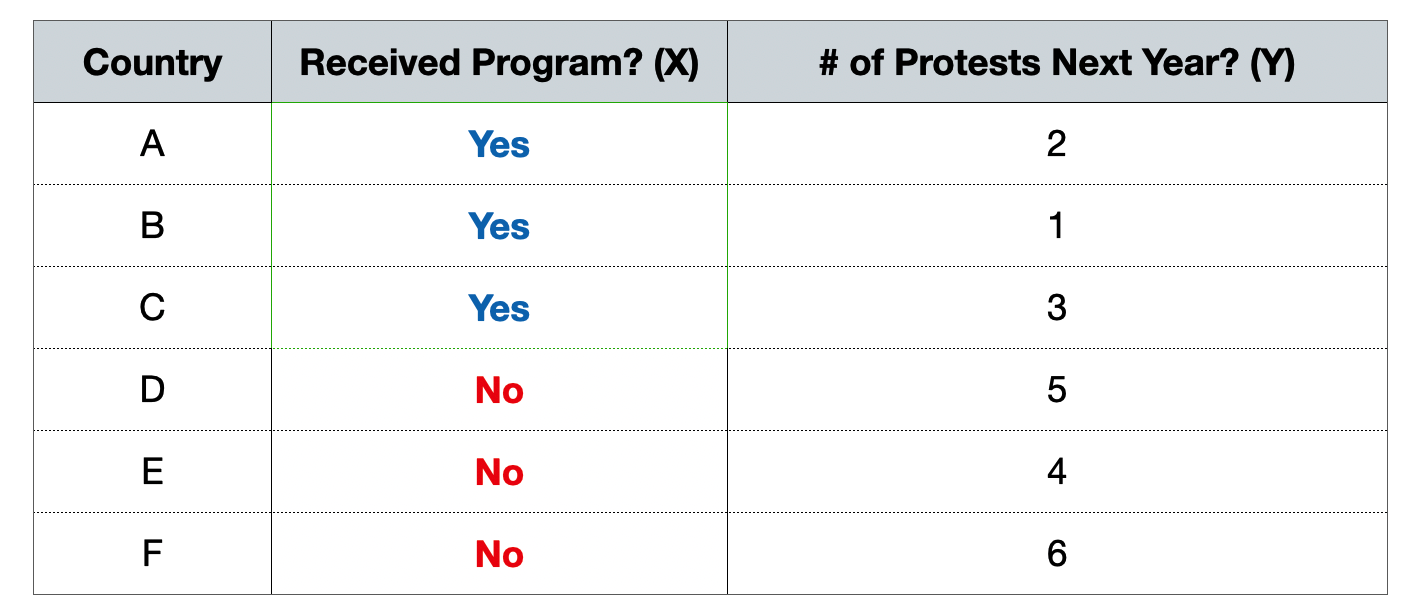
Average protests if received program: (2+1+3)/3 = 2 → fewer protests
Average protests if no program: (5+4+6)/3 = 5 → more protests
what if we knew both worlds?

Counterfactuals

What would Y be if X did not change/take place?

If Trump did not win 2024 elections, would Maduro still be in power?
If it wasn’t for Qatar, would Messi ever win the World Cup?

Potential Outcomes & Counterfactuals

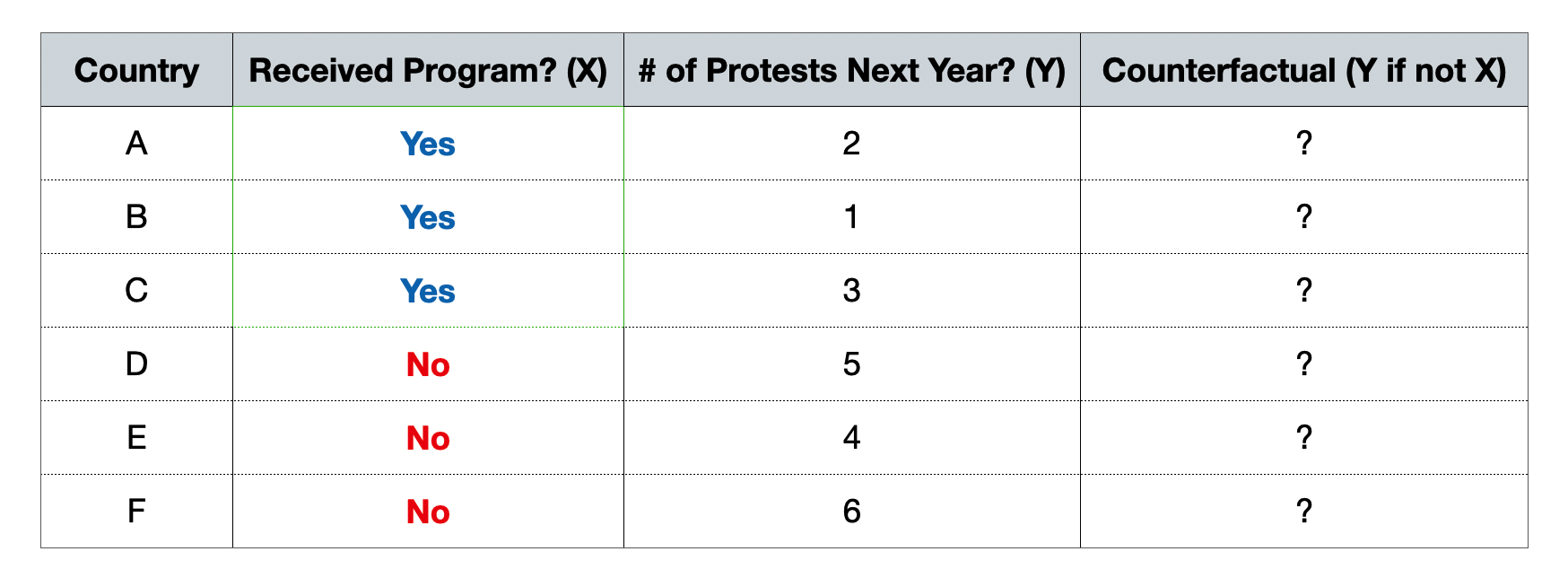
Going back to the example, we do not know the counterfactuals.
But let’s assume we do know them…

Potential Outcomes & Counterfactuals

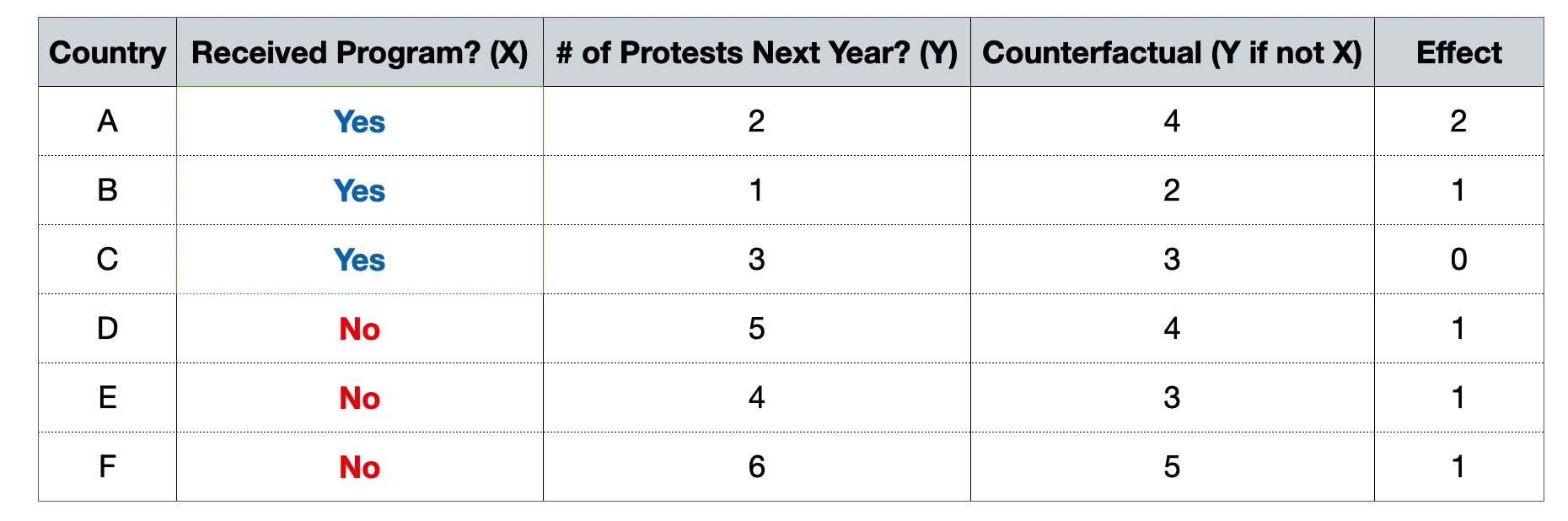
Average effect for countries that received program: (2+1+0)/3 = 1
Average effect for countries that did not receive program: (1+1+1)/3 = 1

Causal Inference

Does a change in X cause a change in Y?

Patterns alone are not enough
- Observations that are treated and not treated tend to be systematically different: Selection bias
Without counterfactuals, it is difficult to make causal claims

How do we detect counterfactuals?

Bad news: we can’t

Fundamental Problem of Causal Inference: We never observe the counterfactual

Good news: we can predict them

Causal inference = imputing the counterfactual and estimating the effect

Imputing the counterfactual

Qualitatively
- Case studies
Quantitatively
- Experiments
- Observational studies

Experiments

Gold standard

Random assignment ensures no selection bias
Isolate the effect of X on Y

Let’s think about this intuitively

An example from a field experiment in Pakistan (Cheema et al. 2022)

How can we close persistent gender gaps in political participation?
- Male household members as “gatekeepers” of women’s participation
Targeting women -> no effect
Targeting male household members -> increase in women’s turnout

Let’s think about this intuitively

An example from a field experiment in Pakistan (Cheema et al. 2022)

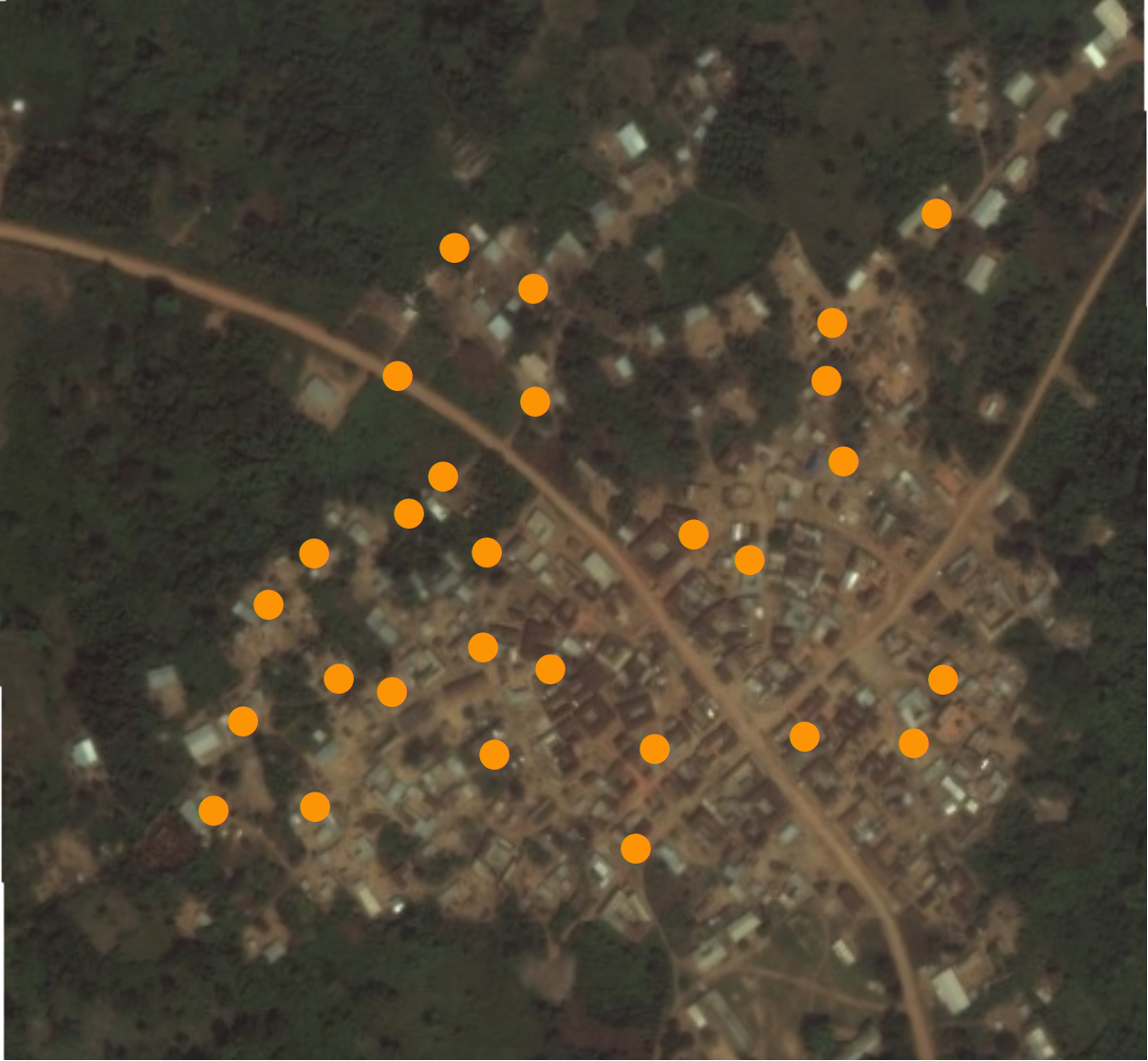
Figure: A random sample of households in Pakistan

Let’s think about this intuitively

An example from a field experiment in Pakistan (Cheema et al. 2022)

Figure: Each household has potential outcomes treated and control

Let’s think about this intuitively

An example from a field experiment in Pakistan (Cheema et al. 2022)

When you assign a household to treated, you are realizing the household’s potential outcome under treatment
When you assign a household to control, you are realizing the household’s potential outcome under control

Let’s think about this intuitively

An example from a field experiment in Pakistan (Cheema et al. 2022)

Random assignment to treated or control means we’re drawing a random sample of these potential outcomes

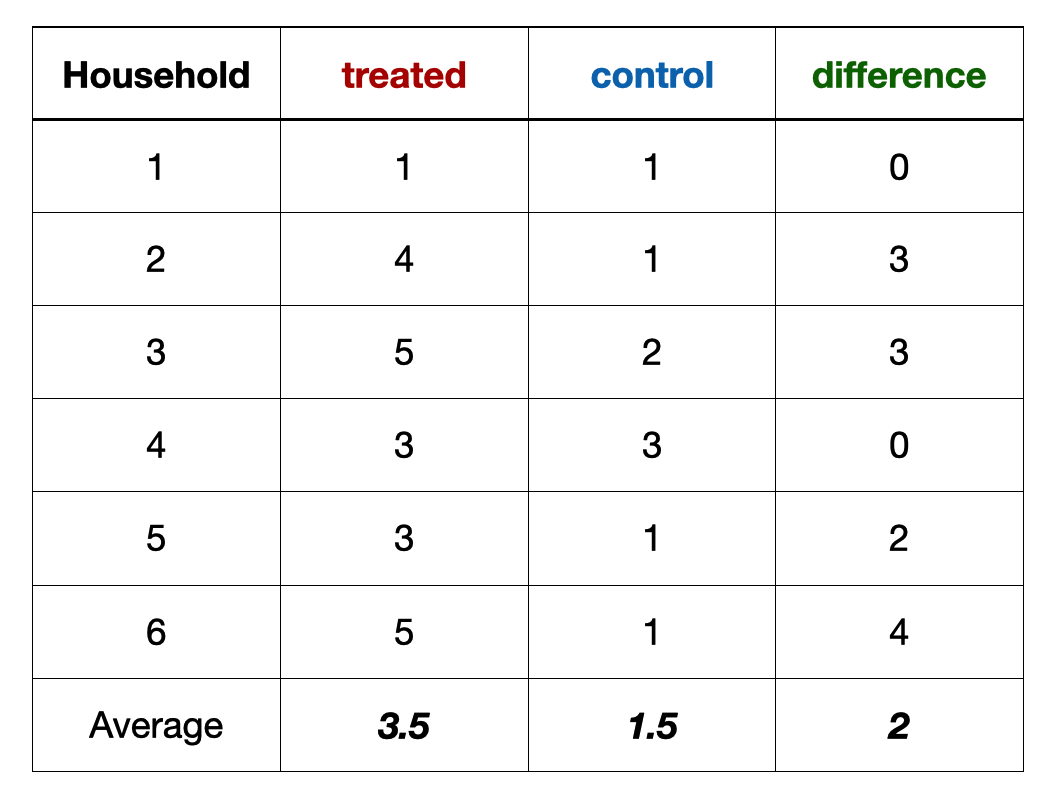
Exercise

An example from a field experiment in Pakistan (Cheema et al. 2022)

Exercise

An example from a field experiment in Pakistan (Cheema et al. 2022)

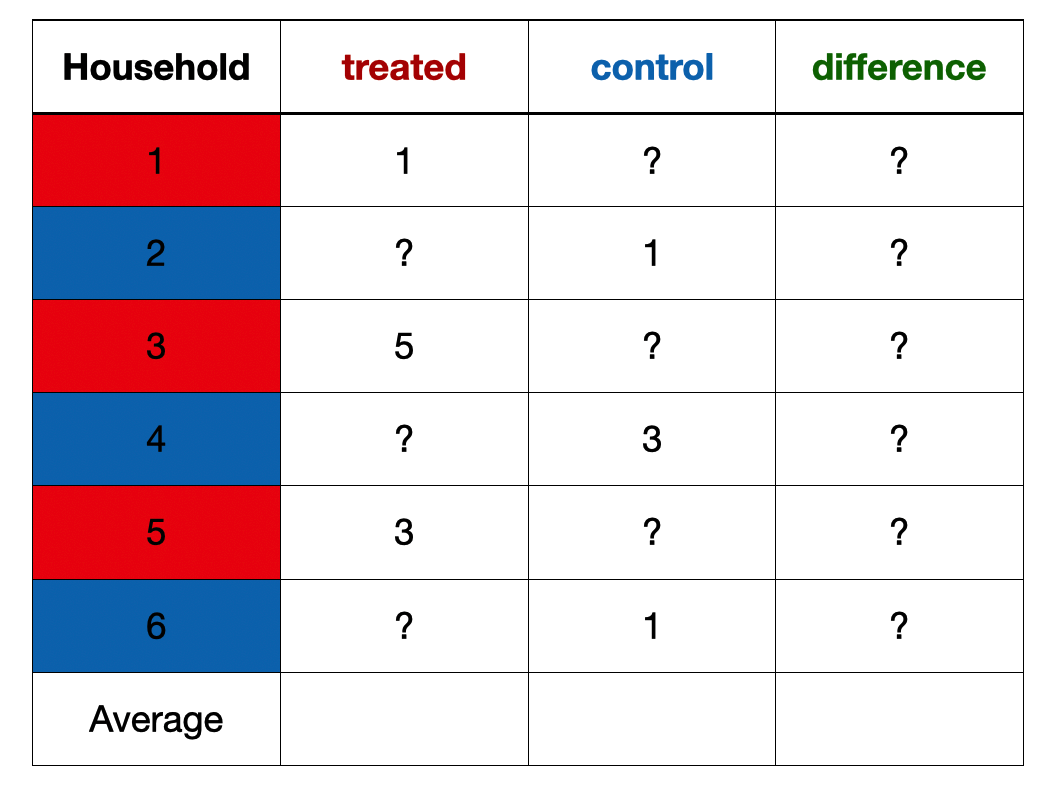
Exercise

An example from a field experiment in Pakistan (Cheema et al. 2022)

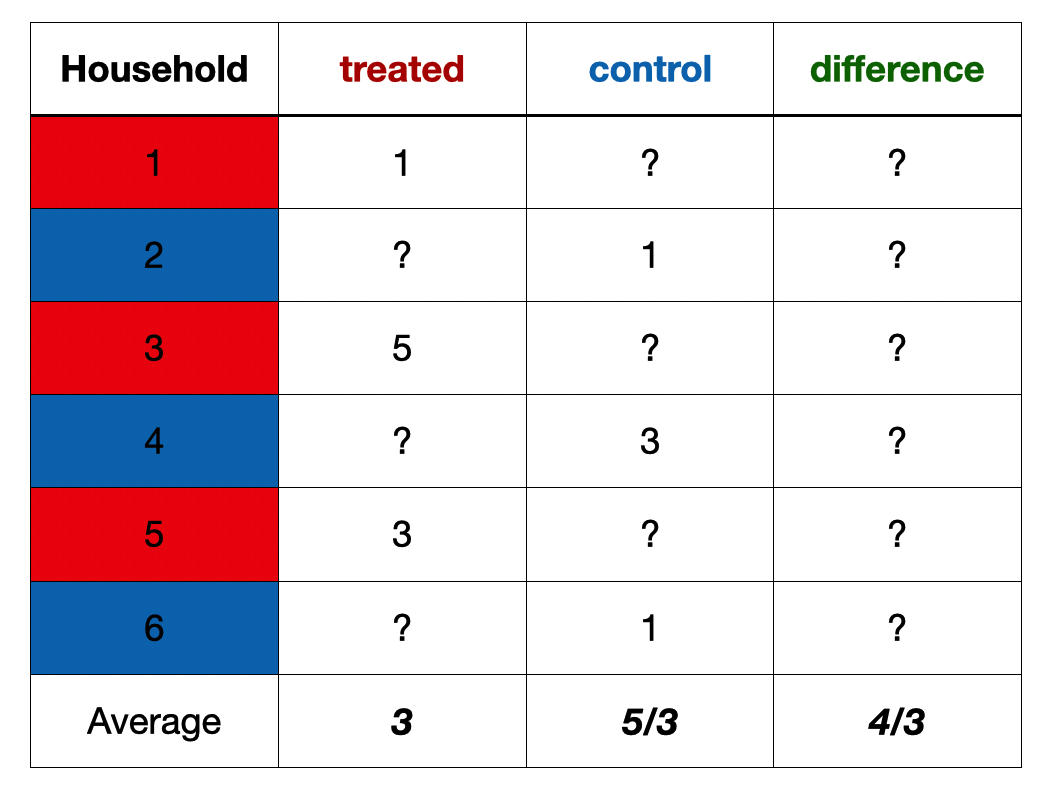
Exercise

An example from a field experiment in Pakistan (Cheema et al. 2022)

Experiments

Limitations

Why not run experiments for everything?
- Practical constraints
  - Cost, time, scale
- Feasibility
  - Cannot randomly assign many social conditions
- Ethical considerations
  - Harm, consent, fairness

Observational Designs

When we cannot run experiments

Many social questions cannot be randomized
- Democracy, migration, welfare, education
Policies are not supposed to be not assigned at random
- Welfare is not given to the rich
This creates selection bias

Matching

Comparing similar units

Idea: Compare units that are similar in important ways, except for whether they received the treatment
Example: Do UN peacekeeping missions reduce civilian deaths?
- Problem: Peacekeepers are sent to more violent conflicts
- Solution: Compare conflicts with similar violence levels
  - Some with peacekeepers | some without

Discontinuity Designs

Comparing units near a cutoff

Some policies use clear rules or thresholds
- Elections, Welfare programs
Example: Does tutoring improve student performance?
Problem: Students who do and do not get tutoring may already be different
Policy: Students scoring 70 or below get tutoring
- Compare students just below and just above 70

Discontinuity designs

Compare units around a threshold

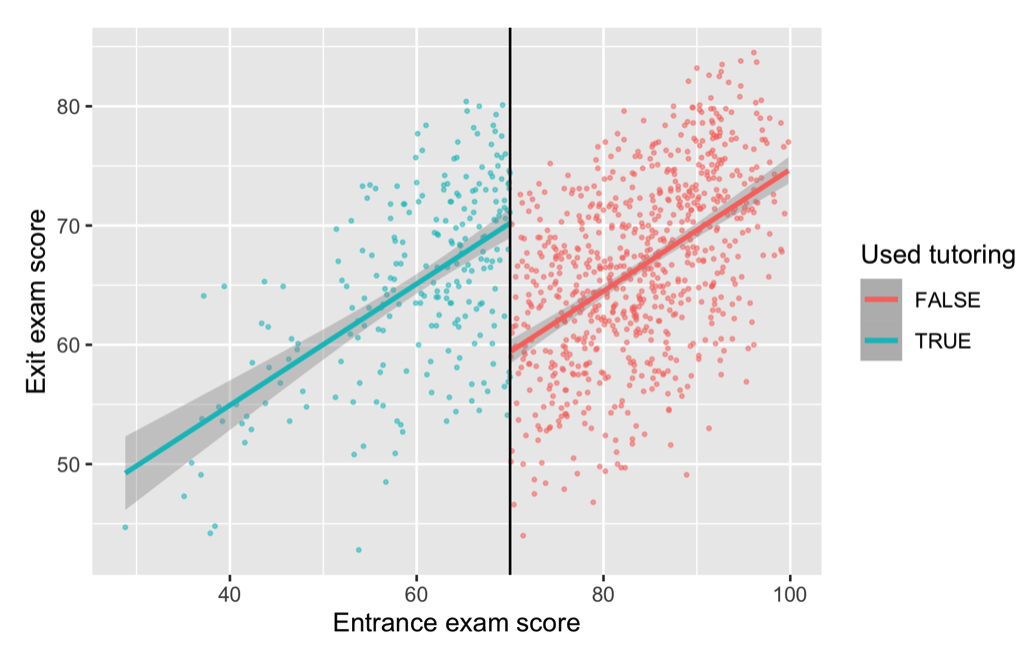
Source: Andrew Heiss

Difference in Differences

Comparing changes over time

Idea:
- Compare how outcomes change over time between a treated group and a similar control group
- Focus on differences in trends, not levels

Difference in Differences

Comparing changes over time

Example: How do sanctions affect human rights violations?
- Two countries:
  - One sanctioned (treated)
  - One not sanctioned (control)
- Key assumption:
  - Both countries followed similar trends before sanctions

Difference in Differences

Compare units that follow similar trends the treatment

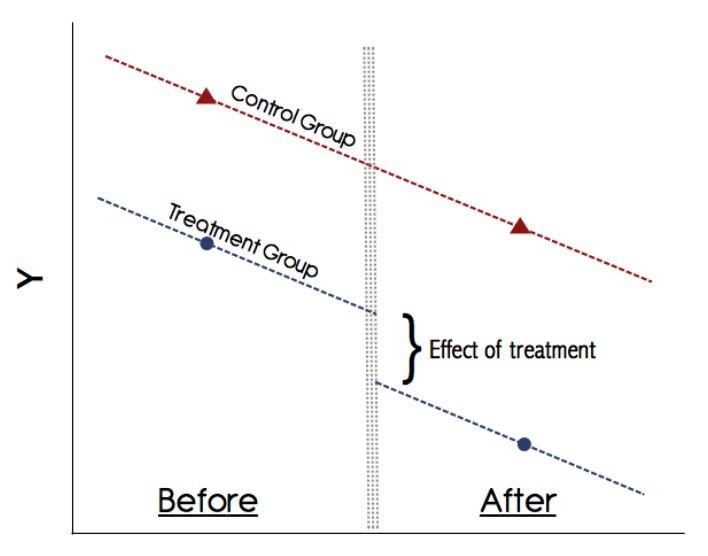
Source: Kevin Goulding

Other designs for observational data

Instrumental variable
Synthetic control
Shared goal: imputing the counterfactual using appropriate the design

Takeaways

Why statistics matters

Data don’t speak for themselves: they are produced, measured, and interpreted by humans.
Statistical reasoning is powerful: bad data, poor comparisons, or naive interpretation can mislead.

Takeaways

Why learn?

Policy relevance: make sense of interventions and their consequences.
Social science literacy: read and critique academic research confidently.
Real-world decision-making: informed skepticism is a marketable skill anywhere data are used.

Thank You

Questions & Discussion

Thank you for your attention!
Feedback, questions, connections: olgahan@brown.edu